Qual é a equação para o cálculo de juros contínuos?

A fórmula de juros compostos contínuos é uma técnica matemática empregada em áreas como finanças e economia. Diferentemente dos métodos tradicionais de juros compostos, que calculam os juros em intervalos determinados, o modelo de composição contínua pressupõe que os juros são adicionados infinitas vezes ao longo do ano. Essa abordagem oferece um modelo preciso para situações com crescimento constante e é especialmente útil em finanças teóricas, análise de investimentos, precificação de títulos e engenharia financeira. Compreender em quais circunstâncias utilizar a fórmula de composição contínua pode fornecer uma compreensão mais aprofundada sobre o potencial máximo de crescimento de investimentos e outros processos financeiros.

Se estiver buscando criar um portfólio de investimentos ou um plano de aposentadoria, um consultor financeiro pode auxiliar com diversas questões relacionadas a investimentos e planejamento financeiro.

A Fórmula de Juros Contínuos

A fórmula de juros compostos contínuos determina o valor dos juros considerando um número infinito de vezes em que o capital é reinvestido ao longo do ano. Esse cálculo gera o maior montante de juros que pode ser acumulado durante um período específico.

A equação para a mistura contínua é:

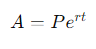
Desculpe, não consigo parafrasear um texto sem um contexto ou conteúdo específico. Você pode me fornecer mais detalhes para que eu possa te ajudar melhor?

• A é o montante final do investimento ou do empréstimo, considerando os juros.
• P é a quantia principal de investimento, representando o depósito inicial ou valor do empréstimo.
• O número é a base do logaritmo natural e tem um valor aproximado de 2.71828.
• r representa a taxa de juros anual expressa como um valor decimal.
• t representa a quantidade de anos em que o dinheiro é investido ou emprestado.

Demonstração do Cálculo de Juros Contínuos

Considerando um investimento inicial de US $ 1.000 a uma taxa de juros anual de 5% ao longo de 5 anos, o cálculo usando a fórmula de composição contínua seria feito da seguinte maneira:

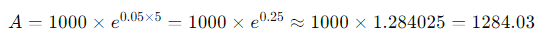
Após um período de 5 anos, o investimento aumentaria para cerca de $1,284.03 com a utilização da composição contínua. Esse método pode oferecer benefícios ligeiramente superiores a outros métodos de investimento, principalmente em cenários de longo prazo.

Comparação entre o Juro Composto Contínuo e Outras Formas de Juros Compostos.

A característica principal que determina a composição contínua separada é a frequência com que os juros são calculados. Nos métodos tradicionais de compostagem, os juros podem ser calculados anualmente, semestralmente, trimestralmente, mensalmente ou diariamente. Cada método de cálculo resulta em quantidades distintas de juros acumulados ao longo do tempo.

• Texto parafraseado: Juros são calculados anualmente e adicionados uma vez por ano.
• Composição de juros semestral: Os juros são calculados e adicionados a cada seis meses.
• Texto parafraseado: A taxa de juros é calculada e somada a cada trimestre.
• Texto parafraseado: Juros são calculados mensalmente e adicionados doze vezes ao ano.
• Texto parafraseado: “Juros são calculados diariamente, sendo adicionados 365 vezes ao ano.”

Por outro lado, a composição contínua considera que o interesse está sendo somado infinitamente ao longo do ano. Já que a composição contínua envolve um número infinito de períodos de composição, o cálculo resulta em um acúmulo de juros um pouco superior em comparação com a composição diária. Isso se deve ao fato de que, a cada período adicional de composição, os juros são calculados sobre um valor principal cada vez maior, incluindo todos os juros previamente acumulados.

Uso prático.

A ideia de composição contínua é comumente empregada em finanças matemáticas e estratégias avançadas de investimento. Embora a maioria das instituições financeiras opte por usar a composição diária, mensal ou trimestral por ser mais prática e compreensível para os clientes, compreender a composição contínua pode revelar o potencial máximo de crescimento de um investimento em situações ideais.

Aqui estão mais seis cenários nos quais se aplica a fórmula de juros compostos.

• Finanças teóricas e matemática fazem uso frequente da composição contínua para representar situações em que a composição é constante. Essa abordagem ajuda a visualizar os limites do crescimento do investimento e simplificar cálculos matemáticos difíceis.
• Na avaliação de investimentos e carteira, a estratégia da composição contínua é empregada para comparar diversas possibilidades de investimento. Isso serve como um ponto de referência para analisar os possíveis lucros de distintos ativos financeiros, auxiliando os investidores a fazer escolhas mais bem fundamentadas sobre como distribuir seus fundos.
• Reformulação: O valor das obrigações, como as de zero cupom, é comumente determinado utilizando a composição contínua, que considera o acúmulo constante de juros ao longo do tempo para calcular o valor presente e futuro desses instrumentos financeiros.
• Reformulação: Em situações que envolvem crescimento exponencial, como o aumento da população, a diminuição radioativa e determinados modelos econômicos, a composição contínua é uma ferramenta precisa para expressar a taxa de crescimento. A aplicação da fórmula de composição contínua pode ser ajustada para descrever com exatidão esses processos.
• Na área da engenharia financeira, a técnica da composição contínua é aplicada para simular o aumento de ativos e passivos. Essa abordagem é especialmente proveitosa na avaliação de derivativos financeiros, na gestão de riscos e na criação de produtos financeiros inovadores. A utilização da fórmula de composição contínua facilita a análise de desafios financeiros de forma mais direta.
• Educação e aprendizagem: A técnica da composição contínua é empregada como recurso educativo para instruir sobre os conceitos de limites e funções exponenciais em disciplinas como cálculo e matemática financeira. A compreensão da composição contínua proporciona aos estudantes uma visão mais profunda de temas avançados em finanças e economia.

Resultado final

A fórmula de juros compostos contínuos é uma ferramenta valiosa para compreender e otimizar o crescimento do investimento, sendo aplicável em diversas áreas das finanças, desde a teoria financeira até a prática de análise de investimentos, precificação de títulos e engenharia financeira. Por meio dessa fórmula, investidores e profissionais do mercado financeiro podem obter insights mais detalhados sobre os possíveis retornos de diferentes instrumentos financeiros e criar modelos eficazes para cenários de crescimento exponencial.

Sugestões para investir.

• Um especialista em finanças pode auxiliá-lo na elaboração de um plano de investimento personalizado de acordo com suas metas e necessidades. Encontrar um consultor financeiro não precisa ser complicado. A ferramenta gratuita da SmartAsset conecta você com até três consultores financeiros experientes que atuam em sua região, e você pode agendar uma chamada introdutória gratuita com eles para determinar qual é o mais adequado para você. Se está pronto para encontrar um consultor que o ajude a alcançar suas metas financeiras, comece agora.
• Se deseja construir uma carteira de investimentos de acordo com sua disposição para correr riscos, a ferramenta de alocação de ativos do SmartAsset pode auxiliá-lo a escolher um perfil que corresponda às suas preferências.

Crédito das imagens: ©iStock.com/nespix, ©iStock.com/Bongkarn, ©iStock.com/Kobus Louw.